Negative Darstellung von Dualzahlen: Einerkomplement und Zweierkomplement bilden

Wenn man sich eine Dualzahl mit einer Bitlänge von 8 Bits anschaut, dann ist der darstellbare Bereich 00000000 - 11111111, womit man die Dezimalwerte 0 - 255 darstellen würde. Was macht man aber, wenn man negative Werte darstellen möchte? Eine Lösung ist, ein Bit für die Darstellung des Vorzeichens zu benutzen, das Vorzeichenbit genannt wird.

Das Vorzeichenbit sollte natürlich nicht irgendwo inmitten der Ziffernfolge stehen, sondern entweder ganz links oder ganz rechts, so dass man es schnell identifizieren kann.

Least Significant Bit

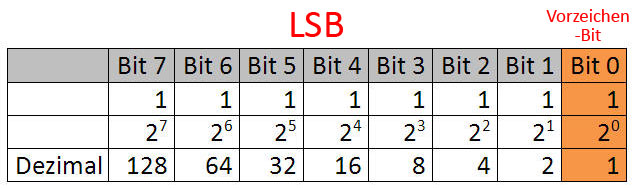
Wenn man die erste Bitstelle von rechts als Vorzeichenbit nimmt, nennt man das Least Significant Bit, da diese Bitstelle die geringste Wertigkeit hat. Deutlich wird das anhand der Tabelle. Bei der Benutzung der ersten Bitstelle als Vorzeichenbit hat man allerdings das Problem, dass die Darstellung der Ziffern nicht den Wertigkeiten entspricht. Beispiel: Man beginnt mit der kleinsten Ziffer, der 1. Die Ziffer 1 links neben dem Vorzeichenbit sollte die Zahl 1 darstellen. Die zweite Bitstelle hat jedoch die Wertigkeit der Dezimalzahl 2. Es wären unnötige Rechenoperationen nötig, um mit den korrekten Zahlen zu arbeiten.

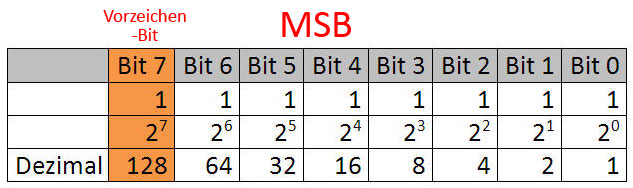
Das erste Bit von rechts eignet sich nicht besonders als Vorzeichenbit. Daher nimmt man das erste Bit von links als Vorzeichenbit. Da diese Bitstelle die höchste Wertigkeit hat, nennt man das Most Significant Bit. Die Ziffern rechts vom MSB würden für die Darstellung der Zahlenwerte genutzt werden. Hierbei wird das MSB wie folgt eingesetzt:

• Positive Zahlen: MSB = 0
• Negative Zahlen: MSB = 1

Eine Bitfolge 10000001 würde die negative Dezimalzahl -1 darstellen, da MSB = 1 ist. Diese Art der Zahlendarstellung nennt man Vorzeichen und Absolutbetrag, da das MSB das Vorzeichen darstellt und die übrigen Zahlenwerte den Absolutbetrag. Hierbei stößt man allerdings wieder auf ein Problem. Für Addition und Subtraktion benötigt man voneinander getrennte Recheneinheiten. Daher hat sich die Komplementbildung mit Einerkomplement und Zweierkomplement etabliert.

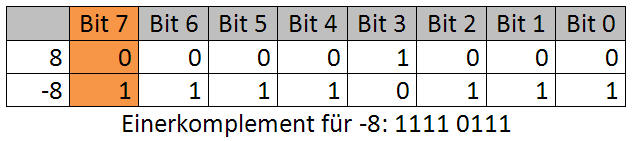
Das Einerkomplement wird gebildet, wenn man alle Ziffern negiert. Aus der Ziffer 0 wird 1, aus der 1 wird 0. Die Darstellung der Dezimalzahl -8 im Einerkomplement wäre 1111 0111. Allerdings hat man auch hier wieder ein Problem. Denn, betrachtet man die Speicherlänge von 8 Bits, dann kann man damit "normalerweise" 256 verschiedene Zahlenwerte (0 - 255) darstellen. Betrachtet man aber die darstellbaren Zahlenwerte im Einerkomplement, dann befinden sich die Zahlenwerte im Bereich -127 (10000000) bis +127 (01111111). Wenn man 2 x 127 multipliziert, ergibt das 254, plus die 0, ergibt 255 verschiedene Zahlenwerte. Wo ist der 256. Zahlenwert geblieben? Eine Zahl muss doppelt vorkommen. Und das ist die 0. Im Einerkomplement kann man für die 0 die Dualzahlen 00000000 oder 11111111 benutzen. Es gäbe eine positive und eine negative 0. Daher wird vom Einerkomplement das Zweierkomplement abgeleitet, um eine Eindeutigkeit zu gewährleisten.

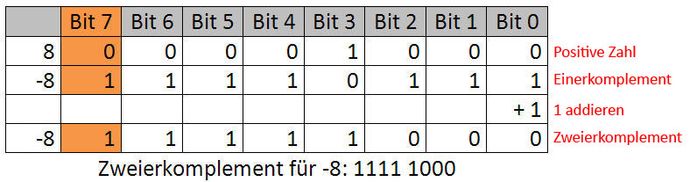
Das Zweierkomplement wird wie folgt gebildet:

• Bilden des Einerkomplements durch negieren aller Ziffern.
• Addition von 1 zum Einerkomplement.

Die negative Zahl -8 hätte im Zweierkomplement folgendes Bitmuster: 11111000. Dadurch erhöht sich auch der darstellbare Zahlenbereich um 1, da die Null nicht mehr doppelt vorkommt. So kann z.B. bei einem Speicherbereich mit 8 Bits die Zahlenwerte -128 bis +127 darstellen.