Schaltalgebra, Boolesche Algebra in der Steuerungstechnik
Bei Speicherprogrammierbaren Steuerungen wird mit den binären Verknüpfungen UND, ODER und NICHT eine Aussagenlogik realisiert. Mit einer Aussagenlogik wird im Grunde eine Schaltfunktion abgeleitet.
Beispiel: Die beiden Taster S1 und S2 müssen gleichzeitig ein Signal 1 liefern, damit die Stanze nach unten bewegt wird.
Es gibt die Möglichkeit, solch eine Aussagenlogik mit Hilfe einer Schaltwerttabelle darzustellen und abzulesen. Alternativ könnte man eine Schaltfunktion auch mit Hilfe einer besonderen Art mathematisch darstellen. Die Darstellung in mathematischer Form nennt man Schaltalgebra. Diese hat ihre Grundlagen in der booleschen Algebra, weshalb auch hier die Gesetze der gewöhnlichen Algebra angewendet werden.
Der Vorteil, eine Schaltfunktion in einen schaltalgebraischen Ausdruck zu bringen ist, dass man diese mathematisch berechnen und mit Hilfe der algebraischen Gesetze umwandeln kann. Ein SPS-Programmierer sollte daher die Schaltalgebra sowie die Gesetze für die Umwandlung eines schaltalgebraischen Ausdrucks kennen.
Ein schaltalgebraischer Ausdruck kann man wie eine mathematische Formel betrachten, z.B. S1 · S2 = Q. Es enthält Variablen, bei der die Buchstaben in Großbuchstaben dargestellt werden. Die Variablen können dabei, bezugnehmend auf das Dualsystem in der Digitaltechnik, nur die beiden Zustände 0 (Aus) oder 1 (An) haben.
Darstellung und Verknüpfungen
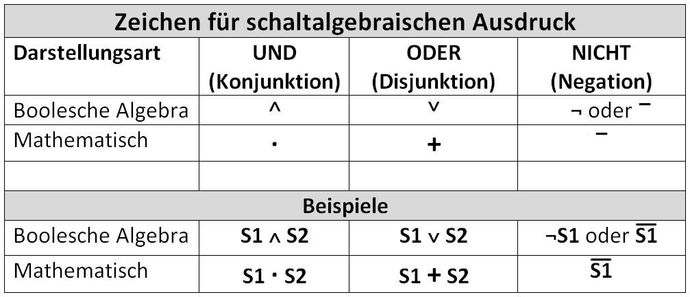
Um eine Aussagenlogik mit den binären Verknüpfungen UND, ODER und NICHT in einem schaltalgebraischen Ausdruck darzustellen, haben sich verschiedene Darstellungsarten etabliert. Hierbei wird grundsätzlich zwischen der Darstellungsart in boolescher Algebra und in mathematischer Form unterschieden.
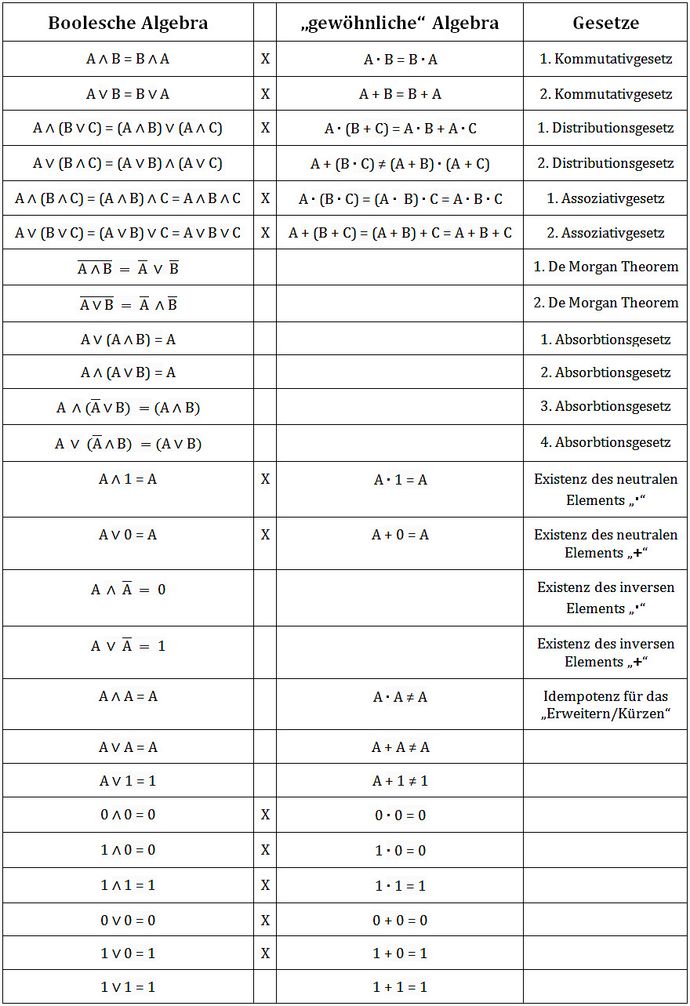
Übersicht über die Gesetze und Eigenschaften der Booleschen Algebra
Kommutativgesetz (Vertauschungsgesetz)
Die Aussagenlogik A UND B UND C ist dasselbe wie C UND A UND B. Das bedeutet, dass in diesem Fall die Variablen vertauscht werden können. Das Vertauschungsgesetz nennt man Kommutativgesetz und kann angewendet werden, wenn alle Variablen durch UND- oder ODER-Gliedern verknüpft sind. In solchen Fällen können die Variablen beliebig vertauscht werden.
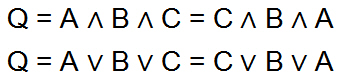
Assoziativgesetz (Verbindungsgesetz)
In der Mathematik kommt die Klammersetzung vor, wenn die Berechnung zweier Variablen zusammengefasst wird. Dabei unterscheidet man zwischen Klammersetzung bei Addition und Klammersetzung bei Multiplikation. Berechnungen, in den die Klammersetzung keine Rolle spielt, sind assoziativ. Das bedeutet, es ist z.B. egal, ob man beim algebraischen Ausdruck A UND B UND C die Berechnung A UND B zusammenfasst oder B UND C. Es ist dem Vertauschungsgesetz ähnlich.
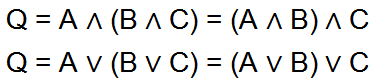
Distributivgesetz (Verteilungsgesetz)
In der Mathematik wird häufig ausgeklammert und ausmultipliziert. Auch in der Schaltalgebra kann, unter Berücksichtigung mathematischer Gesetze, ausgeklammert und ausmultipliziert werden. Ein Ausdruck, der aus UND- oder ODER-Gliedern besteht, kann dabei umgeformt und vereinfacht werden. Die Gesetze der Ausklammerung und Ausmultiplizierung nennt man Distributivgesetz.
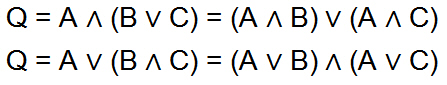
Absorptionsgesetz
Die Variablen eines Ausdrucks können durch die Logik absorbiert, sprich entfernt werden. Wenn man z.B. den Ausdruck betrachtet A ODER (A UND B), dann wird schnell klar, dass es auf B überhaupt nicht ankommt. Denn, für B alleine trifft die Aussage nicht zu, da die Aussagenlogik (A UND B) enthält. Die Aussagenlogik trifft aber zu, wenn A selbst 1 ist, da die Aussagenlogik A ODER enthält. Man kann es auch so formulieren: "B braucht A, A braucht aber B nicht. Daher kommt es alleine auf A an".
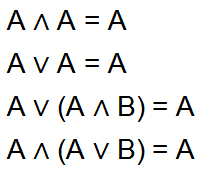
Negationsgesetz
Mit den Negationsgesetzen wird beschrieben was passiert, wenn man die Aussage negiert. Beispiele:
- NICHT A = B ist dasselbe wie A = NICHT B.
- A = NICHT NICHT A
Zu den Negationsgesetzen gehört auch folgende Logik.
- NICHT A UND A ist 0. NICHT A ODER A ist 1.
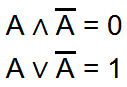
DeMorgan'sche Gesetze
Der englische Mathematiker DeMorgan hat die Gesetze der Schaltalgebra um einige nützliche Gesetze erweitert. Diese neuen Gesetze sind sehr praktisch, insbesondere wenn man negierte Ausdrücke auflösen möchte. Darunter fallen Gesetze für folgende Verknüpfungen:
Für die NAND-Verknüpfung gilt: Eine NAND-Verknüpfung kann aufgelöst werden, indem man das UND-Glied in ein ODER-Glied umwandelt und die Negation auf die einzelnen Variablen anwendet.
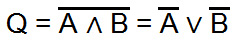
Für die NOR-Verknüpfung gilt: Das Ganze funktioniert auch in die umgekehrte Richtung. Eine NOR-Verknüpfung kann aufgelöst werden, indem man das ODER-Glied in ein UND-Glied umwandelt und die Negation auf die einzelnen Variablen anwendet.
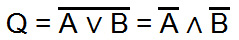
Die Regeln von DeMorgan lassen sich natürlich nicht nur auf NAND- und NOR-Verknüpfungen anwenden. Hierbei wendet man folgende Regeln an:
- Jede einzelne Variable wird negiert.
- Zusätzlich wird der gesamte Term negiert.
- Der Operator UND wird zu ODER, ODER wird zu UND vertauscht.
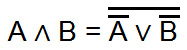
Doppelte Negation
NICHT NICHT A ist dasselbe wie A. Daraus kann man ableiten, dass sich eine doppelte Negation aufhebt. Dies erkennt man auch bei der Umwandlung in NOR- oder NAND-Verknüpfungen. Hierbei geht man wie folgt vor.
Beispiel für eine Umwandlung von einer UND-Verknüpfung in eine NOR-Verknüpfung und wieder zurück in eine UND-Verknüpfung:
- Die UND-Verknüpfung wird doppelt negiert.
- 1. Theorem von De Morgan wird angewendet. Der Operator wird zu ODER, eine Negation wird aufgelöst, die einzelnen Variablen werden negiert und die Schaltung wird zu NOR.
- Wendet man danach das 2. Theorem von De Morgan an, wird der Operator zu UND, die zweite Negation wird aufgelöst und die einzelnen Variablen werden mit diesem Schritt doppelt negiert.
- Die doppelte Negation an beiden Variablen hebt sich auf und die Schaltung wird wieder in eine UND-Verknüpfung umgewandelt.
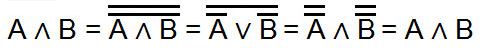
Ausmultiplizieren
Mit dem Absorptionsgesetz können durch Ausmultiplizieren auch Terme zu einem Ausdruck hinzugefügt werden. Beispiel für den Term A ODER (NICHT A UND B). Die Klammern dienen zur Veranschaulichung.
Multipliziert man das aus, erhält man erstmal:
- A ODER A und NICHT A ODER B.
- A UND NICHT A ergibt 1 und kann gestrichen werden.
- Übrig bleibt A ODER B.
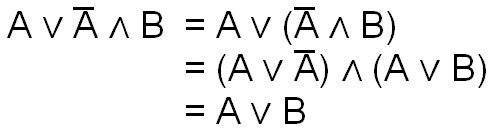
Vorrangregeln und Klammerregeln
Vorrangregeln
Wie in der Mathematik, gibt es auch innerhalb der Schaltalgebra Vorrangregeln, in den festgelegt wird, in welcher Reihenfolge die Operationen durchzuführen sind. Diese sind:
- Negation oder Inversion (NICHT - Verknüpfung)
- Disjunktive Normalform DNF (ODER - Verknüpfung)
- Konjunktive Normalform KNF (UND - Verknüpfung)
Klammerregeln
NOR - Verknüpfung: Eine Klammerung ist nicht notwendig.
UND - Verknüpfung: Eine Klammerung ist nicht notwendig.
ODER - Verknüpfung: Da UND-Verknüpfungen vor ODER-Verknüpfungen gehen (Punkt- vor Strichrechnun), ist eine Klammerung notwendig. Vor allem wenn die Regeln von DeMorgan bei NAND- und NOR-Verknüpfungen angewendet werden, ist eine Klammerung unabdingbar.